The ECM Inspector

Regardless on the way the Extended Confusion Matrix (ECM) has been created, you might want to review it and get some information from it. The ECM Inspector is not a standalone application, but can be invoked from several BF++ Toys, by pressing the "ECM View/Metrics..." button. It looks like the following one:

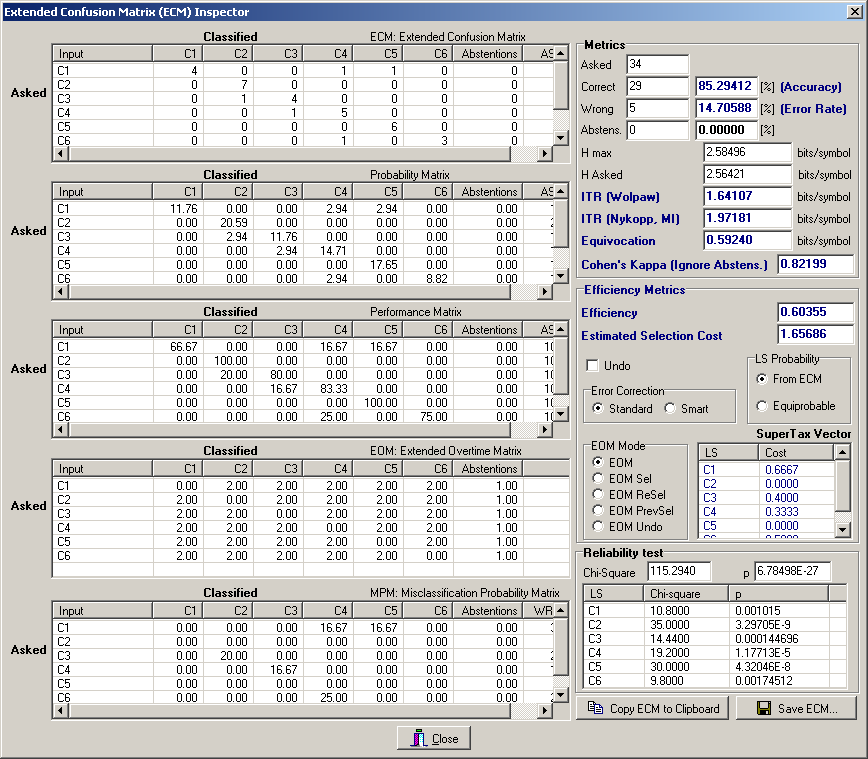
The left side is populated with five different matrices. In each of them on the first rows there are the asked (desired) symbols, whereas on the first column there are the classified (actual) ones. Other rows/columns might be present in each representation.

The matrices are, from top to down:

the Extended Confusion Matrix, in which each elements represents the number of times a combination of asked/classified symbols occurred. The last column (ASKED) represents the sum of all the element of each row (how many time a logical symbol was asked), while the last row represents the sum of all the element of each column (how many times a symbol was classified as such);
the Probability Matrix, which represents the probability (expressed in percentage) for each element of the whole matrix of the ECM to occur;
the Performance Matrix, which represents the probability (expressed in percentage) for each element of each single row of the ECM to occur;
the Extended Overtime Matrix, which represents the costs associated to the recovery of errors (see Bianchi et al. 2007);
the Misclassification Probability Matrix, similar to the Performance Matrix, but relative to file errors only (main diagonal elements are set to zero).

On the right side, instead, there are three groupboxes and two buttons which allow to store into a file or copy to the clipboard the ECM. The three groupboxes are:

1) The Metrics groupbox includes several metrics (computed from the ECM) commonly used in the BCI research field: accuracy, error rate, Information Transfer Rate (ITR), Equivocation and Cohen's Kappa coefficient.

2) The Efficiency Metrics groupbox indicates the Efficiency and other useful parameters (e.g. SuperTax Vector) and settings for its computation (see Bianchi et al. 2007).

3) The Reliability test group, instead, provides a statistical validation of the performances of the classifiers, by comparing the classification accuracies of each symbol against the chance.

The chi-square is a statistical test that is commonly used to evaluate how much the observed distribution of data differs from the expected one, or, in other words, to test the null hypothesis, that states that there is not a significant difference between the observed and the expected results. In our specific case we want to test if the results of a classification are significatively different from the chance level, in order to have an information on the robustness of the achieved accuracy. A statistical evaluation of classification results would suggest us how much we can trust them and is very important for the assessment of mental states.

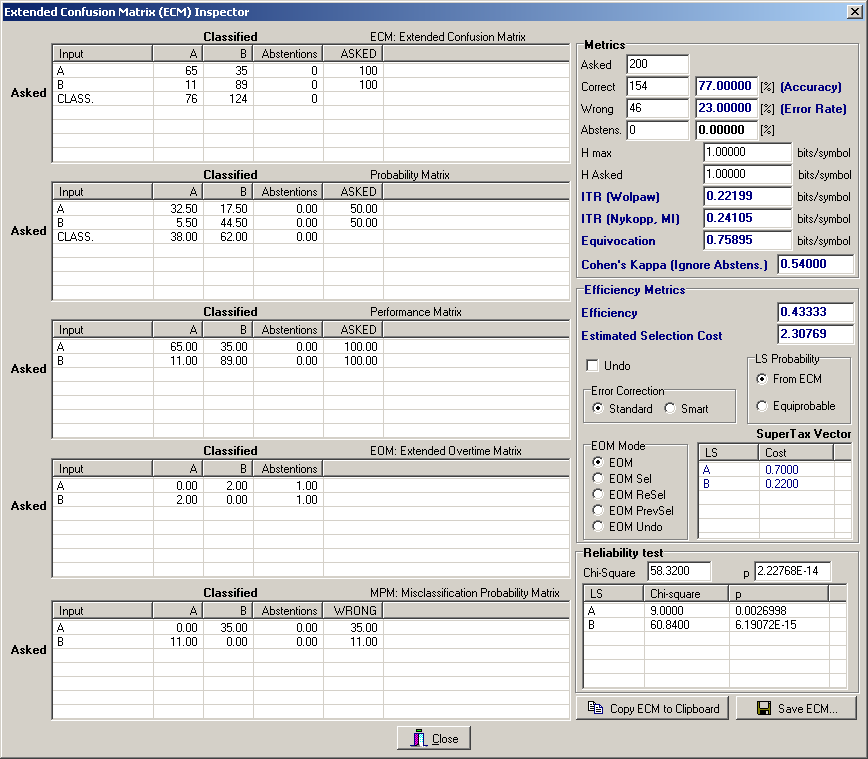
The two main results of a chi-square test are the chi-square value and the p-value: the chi-square value is the sum of the squared difference between observed (o) and the expected (e) data (also known as deviation, d), divided by the expected data, while the p-value sets the significance of the test and so if there is a difference between the observed and the expected cases and that the difference is not due to chance. The chi-square test can be directly applied to classification results that are reported in the confusion matrix. The first step is to detect the number of observed and expected values of each classified class. Therefore, for example suppose to have a binary confusion matrix, see Tab. 1.

	CLASSIFIED
ASKED	A	B
A	65	35
B	11	89

Tab. 1

The overall accuracy is 77%, while the accuracy for class A is 65% and the accuracy of class B is 89%. For class A the number of observed correct items is 65 while the number of expected correct items, which would be due to chance is 50, that means half the total items. Instead the number of observed wrong items is 35 and the number of expected items due to chance is 50. Instead, for class B, the number of observed correct items is 89 while the number of expected correct items is 50. Instead the number of observed wrong items is 11 and the number of expected items due to chance is 50. By applying the test we obtain for class A a chi-value= 9 and a p-value= 0.0027, while for class B we obtain a chi-value= 60.84 and a p.value < 1E-12. This means that for both classes the classifications are statistically different (p<0.01) from the chance level and can help in the assessment of the accuracies of the two classes previously defined.

References

L. Bianchi, L. R. Quitadamo, G. Garreffa, G. C. Cardarilli and M. G. Marciani, “Performances Evaluation and Optimization of Brain-Computer Interface Systems in a copy spelling task”, IEEE Trans Neural Syst Rehabil Eng, vol. 15, no. 2, pp. 207-216, Jun 2007.

Created with the Personal Edition of HelpNDoc: Easy EBook and documentation generator